This UK compound interest calculator enables you to quickly visualise the impact of compounding returns on your investments or savings.
See our guide below if you're calculating compound interest on investments. We offer some ideas on how to project return numbers into the future.
What is compound interest?
Compound interest is the wealth-snowball effect generated by interest earned on interest. Visually the growth of compound interest looks like the green line in this graph:
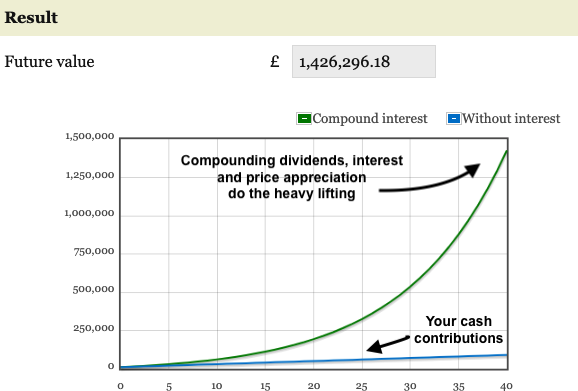
The blue line represents the amount of cash you put into the pot.
The green line is the Miracle-Gro power of dividends, interest, and/or price appreciation over time.
If you leave your investments to accumulate long enough, then your cash contributions are dwarfed by compound growth.
It's like a nuclear chain-reaction. Supply enough feedstock and you can unleash a self-sustaining process of tremendous force.
Compound interest works like this
Imagine an investor puts £1,000 into a fund, gets on with their life, and the fund then merrily grows at 10% per year. The mini-money snowball gathers momentum over time as follows:
| Year | Capital | Interest earned at 10% | New total |
| 1 | £1,000 | £100 | £1,100 |
| 2 | £1,100 | £110 | £1,210 |
| 3 | £1,210 | £121 | £1,331 |
Note: The 10% rate was chosen simply for easy maths!
You earn 20% more on your savings in year three than you did in year one. All without contributing any extra cash beyond that initial £1,000.
Roll the tape on a few more years, and you’d be earning more in annual interest than you first invested. (Inflation notwithstanding.)
These factors juice the return from compound interest:
- Time: Your wealth must compound for years before the snowball builds life-changing speed. That’s why it helps to start investing as soon as you can.
- Interest rate: Small changes in the rate of return make a big difference to your final payout. Equities are the only asset class likely to compound at average rates high enough to produce the wealth lift-off shown by the calculator.
- Fees and taxes: Your compound interest wings are clipped by fees and taxes that shrink your rate of return. Choosing low-cost index funds and maximising your ISAs and SIPPs will offset fees and taxes, respectively.
- Frequency of compounding: The more often interest is paid (e.g. quarterly or monthly), the quicker the compounding effect can get to work.
Note that compound interest rates don’t just refer to interest earned on cash.
Investment returns are also compound interest. They just happen to arrive in the form of dividends and price appreciation.
Gold can also compound so long as its price rises. It’s unlikely to compound at the rate of equities however, as the yellow metal does not cross your hand with dividends or interest.
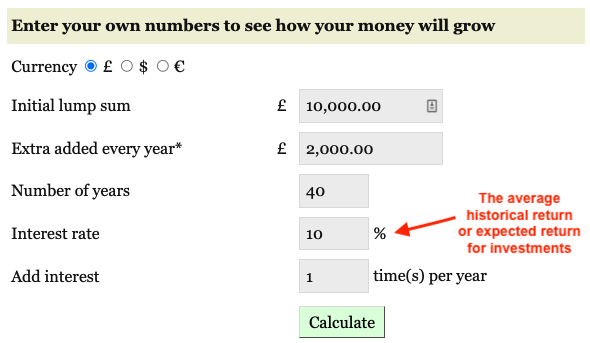
How to use our UK compound interest calculator
Here’s a brief walkthrough for our compound interest calculator, including how to dial in an interest rate that’s suitable for UK investors:
Initial lump sum: this is the amount you’ve saved or invested so far. The total balance of your ISA and SIPP accounts, for example.
Extra added every year: the annual cash contributions you expect to make in the future. For example, if your pension contribution is £200 per month, then pop £2,400 into this field.
Number of years: your investing time horizon. For example, 30 years if you’re a 38-year-old calculating your potential pension pot at age 68.
Add interest: change the figure to 12 for a monthly compound interest rate. It’s 13 for quarterly, 52 for weekly, and 365 for daily compounding.
Interest rate: this is your expected annual return. That's obvious for cash savings. It’s the interest rate you’re currently getting from the bank. But for investments, you’ll have to make a guesstimate. See below.
How to work out your compound interest rate for investments
Two commonly accepted methods of generating a reasonable compound interest rate for investments are:
- Using average historical asset class returns
- Calculating expected returns
Average historical asset returns give us a rough and ready reckoner for the potential performance of different investments over the long-term:
- Global equities can use a 5% average real annualised return
- UK bonds are closer to a 1% average real annualised return
That’s a 3.4% historical average real return for a 60/40 portfolio.
Therefore, you can plug 3.4% into the interest rate field if you’re rocking a 60/40 portfolio.
The expected return method uses a forecast based on investment valuations.
The idea is that incorporating valuation information will produce a projection that’s more accurate than historical performance figures.
Many respected financial institutions issue expected annual return figures for the next 10 to 15 years.
Vanguard’s 2022 10-year annualised nominal returns are:
- UK equities: 4.6%–6.6%
- Global ex-UK equities: 2.8%–4.8%
- UK aggregate bonds: 0.8%–1.8%
Fine-tuning your inputs
You should read up on how to adjust expected return figures for the blend of assets in your portfolio. This will ensure you're entering a sensible growth rate into the 'interest rate' box.
Another option is to calculate your own expected return using the Gordon Equation. It’s surprisingly straightforward.
Read our deep dive into the pros and cons of a standard 60/40 split between equities and bonds to see how to estimate expected returns for your bonds.
Beware that neither of these methods can forecast your personal outcome. Investing is too unpredictable to offer precision.
Expected returns may be more accurate than historical returns but it’s hit and miss. Even ten to 15 years is a relatively short time horizon in investing.
The longer the time period, the more likely it is that investment returns will converge upon their historical average.
That’s why it’s fine to use either method when you’re plotting an event that’s 30 or even 40 years away.
It’s actually a good idea to use both expected returns and historical returns so you have more of a range of outcomes to work with.
If you use nominal returns (unadjusted for inflation) then subtract the long-term, average UK inflation rate.
For example, knock off 3% average UK inflation from a nominal 8% return. Then compound at 5% for an inflation-adjusted result.
Inspiring quotes about compound interest
“My wealth has come from a combination of living in America, some lucky genes, and compound interest.”
– Warren Buffett
“The first rule of compounding: Never interrupt it unnecessarily.”
– Charlie Munger
"Striving for sustained, uninterrupted compounding over long periods of time is smart investing, and that’s precisely our goal. Many people think of us as a “value investor” and others ask whether we are a value or a growth investor. We’ve started to say, we’re neither, we are a compounding investor."
– Chuck Akre
“The tyranny of compounding costs can devastate the miracle of compounding returns.”
– John Bogle
“Relatively small divergences in annual, compounded returns over many years result in dramatic differences in terminal wealth.”
– Nick Train
“Compounding is the magic of investing.”
– Jim Rogers
"Consider the Indians of Manhattan, who in 1626 sold all their real estate to a group of immigrants for $24 in trinkets and beads. For 362 years the Indians have been the subjects of cruel jokes because of it - but it turns out they may have made a better deal than the buyers who got the island. At 8 percent interest on $24 (note: let's suspend our disbelief and assume they converted the trinkets to cash) compounded over all those years, the Indians would have built up a net worth just short of $30 trillion, while the latest tax records from the Borough of Manhattan show the real estate to be worth only $28.1 billion. Give Manhattan the benefit of the doubt: that $28.1 billion is the assessed value, and for all anybody knows it may be worth twice that on the open market. Either way, the Indians could be ahead by $29 trillion and change.. What a difference a couple of percentage point can make, compounded over three centuries"
– Peter Lynch
“Compound interest is the most powerful force in the universe.”
– Albert Einstein (maybe)
“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.”
– Albert Einstein (even less likely he actually said this)
Happy compounding!